A closed 2D shape with four sides, four vertices, and four angles.
Angle Sum Property
The sum of all interior angles of a quadrilateral is \(360°\).
Proof Method:
Divide the quadrilateral into two triangles using a diagonal. Since each triangle sums to \(180°\), \(180° \times 2 = 360°\).
Types of quadrilateral
|
Name
|
Picture
|
Properties
|
|
Parallelogram
|
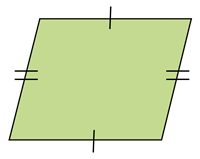 |
1. Opposite sides are equal and parallel.
2. Opposite angles are equal.
3. Diagonals bisect each other.
|
|
Square
|
 |
1. All sides are equal and parallel.
2. All interior angles are 90 ∘ .
3. Diagonals bisect each other at right angles.
|
|
Rectangle
|
 |
1. Opposite sides are equal and parallel.
2. All interior angles are 90 ∘ .
3. Diagonals bisect each other.
|
|
Rhombus
|
 |
1. All sides are equal.
2. Opposite angles are equal.
3. Diagonals are perpendicular.
|
|
Trapezium
|
 |
1. The bases of a trapezium are parallel.
2. Sum of adjacent angles on non-parallel sides are supplementary.
|
|
Kite
|
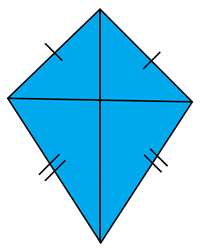 |
1. Diagonals are perpendicular.
2. Diagonals bisect the vertex angles.
3. Non-vertex angles are congruent.
4. Two disjoint pairs of consecutive sides are congruent.
|
Important!
Logical Hierarchy
-
Square \(\subset\) Rectangle \(\subset\) Parallelogram.
-
Square \(\subset\) Rhombus \(\subset\) Parallelogram.
-
All Parallelograms are Trapeziums, but not vice versa.
-
A Kite is not a parallelogram.