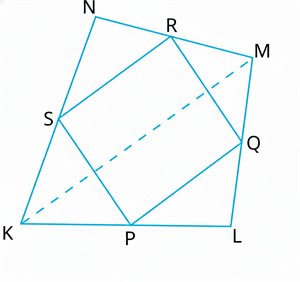
\(KLMN\) is a quadrilateral in which \(P, Q, R\), and \(S\) are mid-points of the sides \(KL, LM, MN\), and \(NK\) (see Fig). \(KM\) is a diagonal.
Show that:
(i) \(SR || KM\) and \(SR =\frac{1}{2}KM\)
(ii) \(PQ = SR\)
(iii) \(PQRS\) is a parallelogram
Given: \(P, Q, R\) and \(S\) are midpoints of quadrilateral \(KLMN\).
(i) To Prove: \(SR || KM\) and \(SR =\frac{1}{2}KM\)
Proof:
Here, taking \(∆KMN\) we can see \(S\) and \(R\) are the mid points of side \(KN\) and \(NM\) respectively. [Given]
By Mid-point Theorem, 'The line segment joining the mid-points of two sides of a triangle is parallel to the third side.'
Hence, and \(SR = \frac{1}{2} KM\) ------\((1)\)
(ii) To Prove: \(PQ = SR\)
Proof:
Now here, taking \(∆KML\) we can see \(P\) and \(Q\) are the mid points of side \(KL\) and \(LM\) respectively. [Given]
By , Mid-point Theorem, 'The line segment joining the mid-points of two sides of a triangle is parallel to the third side.'
Hence, and \(PQ = \frac{1}{2} KM\) ------\((2)\)
From (1) and (2) we can say, .
(iii) To Prove: \(PQRS\) is a parallelogram
From (i) and (ii) we can say that \(PQ || KM\) and \(SR ||KM \) so, and \(PQ = SR\).
Proof:
If each pair of opposite sides of a quadrilateral is , then it is a .
Hence, \(PQRS\) is a parallelogram.