
In trapezium \(ABCD\), \(AB∥DC\) and \(BD\) is a diagonal. Point \(E\) is the midpoint of side\(AD\). A line through \(E\), drawn parallel to \(AB\), meets \(BC\) at \(F\). Show that \(F\) is the midpoint of \(BC\).
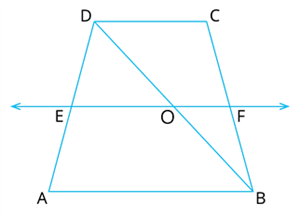
Proof:
Let \(O\) be the point of intersection of lines \(BD\) and \(EF\)
Now, in triangle \(∆ADB\), \(E\) is the mid point of side \(AD\) and \(E\)\(O\)\( || AB\) [Given]
By , 'the line drawn through the mid-point of one side of a triangle, parallel to another side bisects the third side.'
Hence, \(E\)\(O\) \(=\)
In triangle \(∆BCD\), from the above, is the mid point of side \(BD\)
As \(EF ||AB\) & \(AB\parallel CD\)
Therefore, \(EF\parallel \) [Two lines parallel to the same line are parallel to each other]
In \(∆BCD\), \(\parallel CD\) and \(O\) is the midpoint of \(BD\)
Again by converse of Mid-point theorem, 'the line drawn through the mid-point of one side of a triangle, parallel to another side bisects the third side.'
Hence, is the mid-point of \(BC\)
Hence proved.
Answer variants:
\(O\)\(F\)
\(AB\)
\(CD\)
\(O\)
\(F\)