
Given three parallel lines, \(l\), \(m\), and \(n\), and two transversals, \(p\) and \(q\). If transversal \(p\) intersects the lines at points \(A\), \(B\), and \(C\) such that the intercepted segments \(AB\) and \(BC\) are equal in length \((AB=BC)\). Verify that the segments intercepted by the same parallel lines on the other transversal \(q\) are also equal. That is, \(DE=EF\).
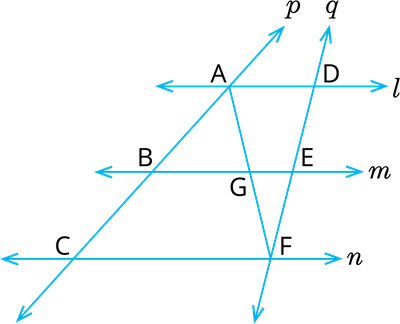
Proof:
Let us join \(A\) to \(F\) intersecting \(m\) at \(G\).
The trapezium \(ACFD\) is divided into two triangles; namely \(∆ ACF\) and \(∆ AFD\).
In \(∆ ACF\), it is given that is the mid-point of \(AC (AB = BC)\) and \(BG ||\) (since \( m||n \)).
Then by converse of Mid-point theorem, 'The line drawn through the mid-point of one side of a triangle, parallel to another side bisects the third side.'
Hence, is the mid-point of \(AF\)
Now, in \(∆ AFD\), we can apply the same argument as \(G\) is the mid-point of \(AF\), \(GE ||\).
Therefore, is the mid-point of \(DF\), [again by using converse of midpoint theorem]
That is, \(DE =\).
In other words, \(l\), \(m\) and \(n\) intercepts of equal measure on \(q\) also.