
Confirm that if the diagonal \(BD\) of rectangle \(ABCD\) bisects \(∠\)\(B\), then \(ABCD\) must be a square.
Proof:
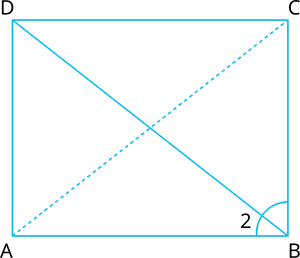
Given that \(ABCD\) is a rectangle.
In \(△BAD\) and \(△DCB\),
\(∠A=∠C=90^°\)
\(BD\) \(=\) ()
\(AB =\) ()
Therefore, \(△BAD≅△\) ()
Thus, \(AB =\) and \(AD =\) (By CPCT)
Therefore, \(AB = BC = CD = AD\).
So, \(ABCD\) is a square.
Hence, proved.