
In trapezium \(PQRS\), where \(PQ||RS\) and \(PS=QR\), show that:
(i) \(\angle P = \angle Q\)
(ii) \(\angle R = \angle S\)
(iii) \(△PQR≅△QPS\)
(iv) Diagonals \(PR\) and \(QS\) are equal in length.
(i) \(\angle P = \angle Q\)
(ii) \(\angle R = \angle S\)
(iii) \(△PQR≅△QPS\)
(iv) Diagonals \(PR\) and \(QS\) are equal in length.
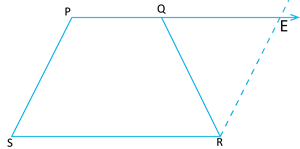
Proof for (i): \(∠P = ∠Q\)
\(PQ || SR\) , \(PE || SR\) Also \(PS || RE\) then,
\(PERS\) is a parallelogram.
Therefore, \(PS = RE\) -----(1) [Opposite sides of the parallelogram are equal]
But \(PS = QR\) [Given] ----(2)
From (1) and (2), \(QR = RE\)
Now, in \(∆QRE\), we have
\(QR = RE\)
\(PERS\) is a parallelogram.
Therefore, \(PS = RE\) -----(1) [Opposite sides of the parallelogram are equal]
But \(PS = QR\) [Given] ----(2)
From (1) and (2), \(QR = RE\)
Now, in \(∆QRE\), we have
\(QR = RE\)
\(∠REQ = ∠RQE\) ----(3)
Also, \(∠PQR + ∠RQE = 180^°\) ----(4) [] and
\(∠P + ∠REQ = 180^°\) ----(5) [Co-interior angles of a parallelogram PSRE]
From (4) and (5), we get
\(∠PQR + ∠RQE = ∠P + ∠REQ\)
\(∠PQR = ∠P\) [From (3)]
\(∠Q = ∠P\) -----(6)
From (4) and (5), we get
\(∠PQR + ∠RQE = ∠P + ∠REQ\)
\(∠PQR = ∠P\) [From (3)]
\(∠Q = ∠P\) -----(6)
Proof for (ii): \(∠R = ∠S\)
\(PQ || RS\) and \(LO\) is a transversal.
\(∠P + ∠S = 180^°\) ------(7) []
Similarly, \(∠Q + ∠R = 180^°\) -------(8)
From (7) and (8), we get
\(∠P + ∠S = ∠Q + ∠R\)
\(∠R = ∠S\) [From (6)]
From (7) and (8), we get
\(∠P + ∠S = ∠Q + ∠R\)
\(∠R = ∠S\) [From (6)]
Proof for (iii): \(∆PQR ≅ ∆QPS\)
In \(∆PQR\) and \(∆QPS\), we have
\(PQ = QP\) [Common]
\(QR = PS\) [Given]
\(∠PQR = ∠QPS\) [Proved]
\(PQ = QP\) [Common]
\(QR = PS\) [Given]
\(∠PQR = ∠QPS\) [Proved]
Hence, \(∆PQR ≅ ∆QPS\) []
Proof for (iv): Diagonal \(PR =\) Diagonal \(QS\)
Since, \(∆PQR ≅ ∆QPS\) [Proved]
\(PR = QS\) []