
Prove that for a square \(ABCD\), any line segment \(PQ\) that connects a point \(P\) on side \(AD\) to a point \(Q\) on side \(BC\) and passes through the center \(O\) of the square's diagonals. Prove that \(O\) divides \(PQ\) into two equal parts.
Given: \(ABCD\) is a square whose diagonals bisect each other at \(O\).
Proof:
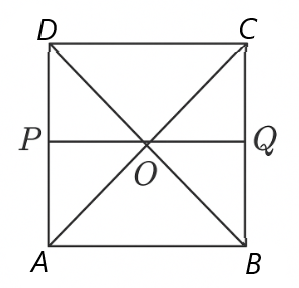
In \(△ODP\) and \(△OBQ\) ,
\(∠BOQ=\) []
\(∠OBQ=\) [] and
\(OB =\) []
Therefore, \(△ODP≅△OBQ\) []
Hence, \(OP=\) [CPCT rule].
\(∠BOQ=\) []
\(∠OBQ=\) [] and
\(OB =\) []
Therefore, \(△ODP≅△OBQ\) []
Hence, \(OP=\) [CPCT rule].
Therefore, Therefore \(O\) divides \(PQ\) into two equal parts
Answer variants:
ASA congruence rule
diagonals bisect each other
alternate interior angles
CPCT rule
Vertically oppsoite angles