
\(G\) and \(H\) are points on diagonal \(AC\) of a parallelogram \(ABCD\) such that \(AG=CH\). Show that \(BHDG\) is a parallelogram.
Join \(BD\), meet \(AC\) at point \(O\).
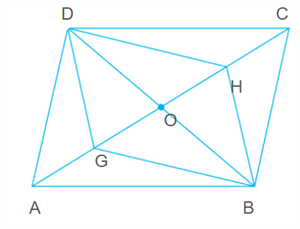

Since, the diagonals of a parallelogram bisect each other.
Therefore, \(OA\)\(=\) and \(OD\)\(=\)\(OB\)
Now, \(OA\)\( = \) and \(AG\)\(= \) \(CH\)
Now, \(OA\)\(−\)\(AG\)\(=\)\(OC\)\(−\) \(CH\)
That is, \(OG=\)
Thus, \(BHDG\) is a quadrilateral whose bisect each other.
Therefore, \(BHDG\) is a parallelogram.
Hence, proved.