
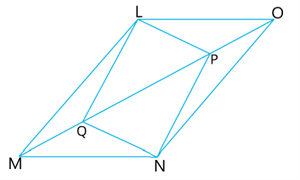
In parallelogram \(LMNO\), two points \(P\) and \(Q\) are taken on diagonal \(MO\) such that \(O P= MQ\) (see Fig.).
Justify that :
(i) \(∆LPO ≅ ∆NQM\)
(ii) \(LP = NQ\)
(iii) \(∆LQM ≅ ∆NPO\)
(iv) \(LQ = NP\)
(v) \(LPNQ\) is a parallelogram
Solution:
Given:
In parallelogram \(LMNO\), two points \(P\) and \(Q\) are taken on diagonal \(MO\) such that \(O P= MQ\)

(i) To Prove: \(∆LPO ≅ ∆NQM\)
Proof:
As \(LMNO\) is a parallelogram.
\(∠LOM =∠ NMO\) [] ------(1)
\(∠LMO = ∠NOM\) [] ------(2)
Now, in \(∆LPO \)and \(∆NQM\), we have
\(LO=\) [Opposite sides of a parallelogram\(LMNO\) are equal]
\(PO =\) [Given]
\(∠LOP= ∠NMQ\) [alternate interior angles are equal]
Hence, \(∆LPO ≅ ∆NQM \) [By ]
(ii) To Prove: \(LP = NQ\)
Proof:
As, \(∆LPO ≅ ∆NQM\) [from (i)]
\(LP =\) [By C.P.C.T.] ----(3)
(iii) To Prove: \(∆LQM ≅ ∆NPO\)
Proof:
Now, in \(∆LQM\) and \(∆NPO\), we have
\(QM =\) [Given]
\(∠LMQ =∠NOP\) [Alternate interior angles are equal]
\(LM = NO\) [ Opposite sides of a parallelogram \(LMNO\) are equal]
Hence, \(∆LQM≅ ∆NPO \)[By ]
(iv) To Prove: \(LQ = NP\)
As, \(∆LQM ≅ ∆NPO \) [from (iii)]
Proof:
\(LQ =\) [] ------(4)
(v) To Prove: \(LPNQ\) is a parallelogram
In a quadrilateral \(LPNQ\),
Proof:
Opposite are equal. [From (3) and (4)]
We know that, If each pair of opposite sides of a quadrilateral is equal, then it is a parallelogram.
Hence, \(LPNQ\) is a parallelogram.