
1. Angles of a quadrilateral are in the ratio \(3:3:4:5\). Obtain all the angles of the quadrilateral.
The required angles are \(^\circ\),\(^\circ\),\(^\circ\),\(^\circ\).
[Note: Enter the answer in ascending order]
2. In Fig., If \(AX\) and \(CY\) are internal bisectors of opposite angles \(A\) and \(C\) of a parallelogram \(ABCD\), establish that \(AX\) is parallel to \(CY\).
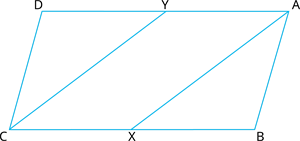
Solution:
\(∠A = ∠C\) (Opposite angles of parallelogram \(ABCD\))
Therefore, \(\frac{1}{2} ∠A = \frac{1}{2} ∠C\) [Since, \(AX\) and \(CY\) are the angle bisectors of angles \(A\) and \(C\) respectively]
That is, \(∠YAX = ∠\)-------- (1)
Also, \(∠AYC + ∠YCX =\) \(^o\) (Because \(YA || CX\)) ----(2)
Therefore, \(∠AYC + ∠YAX = 180^o\) [From (1) and (2)]
So, \(AX || CY\) (As interior angles on the same side of the transversal are supplementary)