
\(AB\) and \(CD\) are two equal and parallel line-segments. Any point \(M\) not lying on \(AB\) or \(CD\) is joined to \(N\) and \(D\) and lines through \(A\) parallel to \(BM\) and through \(C\) parallel to \(DM\) meet at \(N\). Prove that line segments \(MN\) and \(AB\) are equal and parallel to each other.
Proof:
We draw the figure as per the given conditions
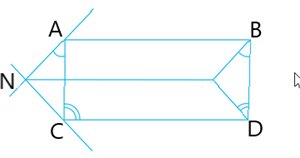
It is given that \(AB = CD\) and \( AB||CD\).
Therefore, \(ABDC\) is a parallelogram.
So, \(AC = \) and \(AC || BD\)---- (1)
Now, \(AC || BD\)
Therefore, \(∠CAB + ∠ABD =\) \(^o\) (Interior angles on the same side of the transversal)
i.e., \(∠CAB+ ∠ABM + ∠MBD = 180^o\)--- (2)
Also, \(AN || BM\) (By construction)
Therefore, \(∠NAB + ∠\) \(= 180^o\)
That is, \(∠NAC + ∠CAB + ∠ABM = 180^o\)--- (3)
So, \(∠NAC = ∠\) [From (2) and (3)] ----(4)
Similarly, \(∠NCA = ∠\) ----(5)
Therefore, \(∆ANC ≅ ∆BMD\) [, using (1), (4) and (5)]
So, \(AN =\) and \(NC =\) (CPCT)
As, \(AN = BM\) and \(AN || BM\), we have \(ABMN\) is a parallelogram
So, \(MN = AB\) and \(NM || AB\).