
Consider a parallelogram \(LMNO\) in which the diagonal \(LM\) bisects one of its angles \(\angle A\). Verify that it is a rhombus
Proof:
Consider a parallelogram \(LMNO\) such that its diagonal \(LN\) bisects \(∠L\).
Thus, \(∠NLM=∠NLO\) .....(1)
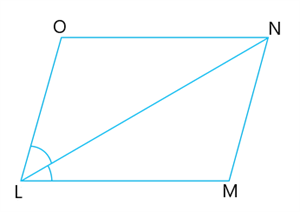
To Prove: \(LMNO\) is a rhombus.
Explanation:
Given, \(LMNO\) is a parallelogram.
Therefore, \(LM || NO\) and is the transversal.
Therefore, \(∠NLM=∠\) []
Again, \(LO || MN\) and \(LN\) is the transversal.
Therefore, \(∠NLO=∠\) []
So, \(∠LNO=∠LNM\) [Since, \(∠NLM=∠NLO\)] .....(2)
Also, \(∠L=∠N\) [opposite angles of parallelogram are equal]
\(\frac{1}{2}∠L=\frac{1}{2}∠\)
From (1) and (2)
\(∠NLO=∠\)
\(NO=\) [sides opposite to the equal angles are equal]
As, \(LM = NO\) and \(LO = MN\) [opposite side of parallelogram are equal]
Therefore, \(LM = MN = NO = LO\)
Thus, all sides are equal.
So, \(LMNO\) is a rhombus.
Hence, proved.