\(AB\) is a line-segment. \(P\) and \(Q\) are points on opposite sides of \(AB\) such that each of them is equidistant from the points \(A\) and \(B\). Show that the line \(PQ\) is the perpendicular bisector of \(AB\).
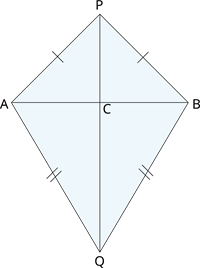
Proof:
Let us take \(∆ PAQ\) and \(∆ PBQ\).
\(∆ PAQ ≅ ∆ PBQ\) ( rule)
Therefore, \(∠ APQ = ∠ BPQ\) (By).
Now let us consider \(∆ PAC\) and \(∆ PBC\).
\(∆ PAC ≅ ∆ PBC\) ( rule)
Therefore, \(AC = BC\) () ------(1) and
\(∠ ACP = ∠ BCP\) ()
\(∠ ACP = \)\(^°\)---- (2)
From (1) and (2), we can easily conclude that \(PQ\) is the perpendicular bisector of \(AB\).
Hence, we proved.