\(∆ ABC\) and \(∆ DBC\) are two isosceles triangles on the same base \(BC\) and vertices \(A\) and \(D\) are on the same side of \(BC\) (See the following Figure)
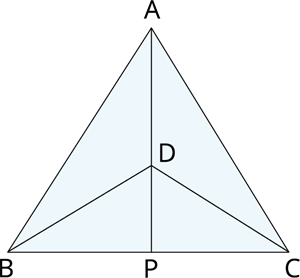
If \(AD\) is extended to intersect \(BC\) at \(P\), show that
(i) \(∆ ABD ≅ ∆ ACD\)
(ii) \(∆ ABP≅ ∆ ACP\)
(iii) \(AP\) bisects \(∠ A\) as well as \(∠ D\).
(iv) \(AP\) is the perpendicular bisector of \(BC\).
Proof :
(i) \(∆ABD ≅ ∆ACD\) [By Congruence rule]-----1
(ii) \(∆ABP≅∆ACP\) [By rule]
(iii) \(∠BAD = ∠\) [By CPCT] (from 1)
Hence, \(AP\), bisects \(∠A\)
\(∆BDP≅∆CDP\) (By Congruence rule)
\(∠BDP=∠\) (By CPCT)
Hence \(DP\) bisects \(∠D\) and \(AP\) bisects \(∠D\)
\(AP\) bisects \(∠A\) as well as \(∠D\).
(iv) \(∠APB=∠\) \( [∆ABP≅∆ACP\) by \(C.P.CT]\)
\(∠APB=\) \(^°\)