In a triangle \(ABC\), \(D\) is the mid-point of side \(AC\) such that \(BD = \frac{1}{2} AC\). Show that \(\angle ABC\) is a right angle.
Proof:
Given that in \(\triangle ABC\), \(D\) is the mid-point of side \(AC\) such that \(BD = \frac{1}{2} AC\).
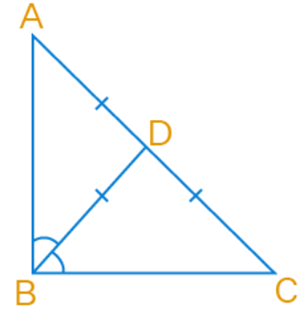
\(AD = \) [Since \(D\) is the midpoint]
Now, \(AC = AD + DC\)
\(AC = AD + AD\) or \(AC = DC + DC\)
\(AC = 2AD\) or \(AC = 2DC\)
\(AD = DC = \frac{1}{2} AC\) ---- (\(1\))
\(BD = \frac{1}{2} AC\) ---- (\(2\)) [Given]
From (\(1\)) and (\(2\)), we have:
\(AD =\) \(= BD\) ---- (\(3\))
In \(\triangle DAB\),
\(AD = BD\) [From (\(3\))]
We know that, the angles opposite to sides are equal
\(\angle DAB = \angle DBA\) ---- (\(4\))
Similarly, in \(\triangle DCB\),
\(BD = DC\) [From (\(3\))]
\(\angle DBC = \angle \) ---- (\(5\)) [Angles opposite to equal sides are equal]
Applying angle sum property in \(\triangle ABC\), we have:
\(\angle ABC + \angle BAC + \angle ACB = 180^{\circ}\)
\(\angle ABC + \angle BAD + \angle DCB = 180^{\circ}\) [From the figure \(\angle BAC = \angle BAD\) and \(\angle ACB = \angle DCB\)]
\(\angle ABC + \angle DBA + \angle DBC = 180^{\circ}\) [Using (\(4\)) and (\(5\))]
\(\angle ABC + \angle ABC = 180^{\circ}\) [Since \(\angle ABD + \angle DBC = \angle ABC\)]
\(2 \angle ABC = 180^{\circ}\)
\(\angle ABC = \)\(^{\circ}\)
Therefore, \(\angle ABC\) is a right angle.
Hence, we proved.