The image of an object placed at a point \(A\) before a plane mirror \(LM\) is seen at the point \(B\) by an observer at \(D\) as shown in the below figure. Prove that the image is as far behind the mirror as the object is in front of the mirror.
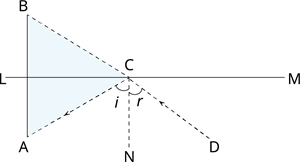
[Hint: \(CN\) is normal to the mirror. Also, angle of incidence \(=\) angle of reflection].
Proof:
Let \(O\) denote the intersection of the lines \(AB\) and \(LM\). Let us prove that \(AO = BO\).
Here, \(\angle i = \angle r\) ---- (\(1\)) [Since angle of incidence \(=\) angle of reflection]
\(\angle CBO = \angle i\) ---- (\(2\)) [Corresponding angles]
\(\angle CAO = \angle r\) ---- (\(3\)) [Alternate interior angles]
From equations (\(1\)), (\(2\)) and (\(3\)), we have:
\(\angle CBO = \angle \) ---- (\(4\))
In \(\triangle BOC\) and \(\triangle AOC\), we have:
\(\angle BOC = \angle AOC =\) \(^{\circ}\)
\(OC = OC\) [Common side]
\(\angle CBO = \angle CAO\) [From (\(4\))]
Thus, by congruence rule\(\triangle BOC \cong \triangle AOC\)
Therefore, by , \(AO = BO\)
Hence, we proved.