In quadrilateral \(ACBD\), \(AC = AD\) and \(AB\) bisects \(∠ A\).
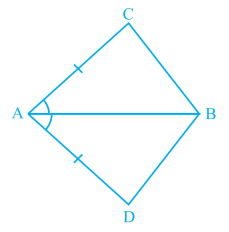
Show that \(∆ ABC ≅ ∆ ABD\). What can you say about \(BC\) and \(BD\)?
Proof:
In \(ΔABC\) and \(ΔABD\), we have:
\(AC =\) [given] --- (1)
\(∠CAB = ∠\) (As \(AB\) bisects \(∠A\)) ----(2)
\(AB = AB\) (Common side) -----(3)
Therefore, by congruence rule, \(ΔABC ≅ ΔABD\).
Thus, by \(CPCT\), \(BC\)\(BD\).