In Fig., \(OA = OB\) and \(OD = OC\). Show that
(i) \(∆ AOD ≅ ∆ BOC\) and
(ii) \(AD || BC\)
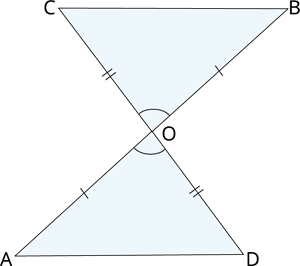
Proof:
(i) In \(∆ AOD\) and \(∆ BOC\),
\(OA = OB\) [Given]
\(OD = OC\) [Given]
\(\angle AOD = \angle\) ( )
Thus, \(∆ AOD ≅ ∆ BOC\) (by the congruence rule),
Hence proved
(ii) In \(\triangle AOD\) and \(\triangle BOC\), we have:
\(∠ OAD = ∠ OBC\) []
Therefore, \(AD \parallel BC\).
Hence, we proved.