Two sides \(AB\) and \(BC\) and median \(AM\) of one triangle \(ABC\) are respectively equal to sides \(PQ\) and \(QR\) and median \(PN\) of \(∆ PQR\).
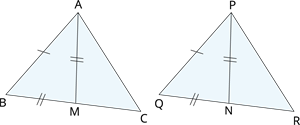
Show that:
(i) \(∆ ABM ≅ ∆ PQN\)
(ii) \(∆ ABC ≅ ∆ PQR\)
Answer:
In \(ΔABM\) and \(ΔPQN\)
\(\frac{1}{2}BC =\frac{1}{2}QR\)
\(BM\) =
\(ΔABM ≅ ΔPQN\) ( Rule)
\(∠B=∠\) [c.p.c.t]
(II) Now in \(ΔABC\) and \(ΔPQR\)
\(ΔABC ≅ PQR\) rule