\(ABC\) is a right triangle such that \(AB = AC\) and bisector of angle \(C\) intersects the side \(AB\) at \(D\). Prove that \(AC + AD = BC\).
Proof:
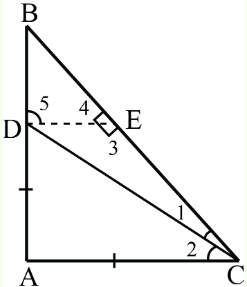
In \(\triangle DAC\) and \(\triangle DEC\), we have:
\(\angle 1 = \angle 2\) [\(CD\) is the bisector of \(\angle C\)]
\(DC = DC\) [Common side]
\(\angle A = \angle 3 = \)\(^{\circ}\)
Thus, by congruence rule\(\triangle DAC \cong \triangle DEC\)
So, \(DA = DE\) ---- (\(1\)) [By CPCT]
And, \(AC = EC\) ---- (\(2\)) [By CPCT]
In \(\triangle ABC\), we have:
\(AB = AC\) [Given]
\(\angle B = \angle C\) ---- (\(3\)) [Angles opposite to equal sides are equal]
Applying angle sum property in \(\triangle ABC\), we get:
\(\angle A + \angle B + \angle C =\) \(^{\circ}\)
\(90^{\circ} + \angle B + \angle B = 180^{\circ}\) [Using (\(3\))]
\(90^{\circ} + 2 \angle B = 180^{\circ}\)
\(2 \angle B = 180^{\circ} - 90^{\circ}\)
\(2 \angle B =\) \(^{\circ}\)
\(\angle B = 45^{\circ}\)
Applying angle sum property in \(\triangle BED\), we get:
\(\angle B + \angle E + \angle D = 180^{\circ}\)
\(45^{\circ} + 90^{\circ} + \angle D = 180^{\circ}\)
\(135^{\circ} + \angle D = 180^{\circ}\)
\(\angle D = 180^{\circ} - 135^{\circ}\)
\(\angle D =\)\(^{\circ}\)
Thus, \(\angle B = \angle D = 45^{\circ}\)
So, \(BE = DE\) ---- (\(4\)) [Sides opposite to equal angles are equal]
\(\Rightarrow DA = DE = BE\) ---- (\(5\)) [Using (\(1\)) and (\(4\))]
We know that \(BC = BE + EC\)
\(BC = DA + \) [Using (\(2\)) and (\(5\))]
Therefore, \(AC + AD = BC\).
Hence, we proved.