In an isosceles triangle \(PQR\) with \(PQ= PR\), \(X\) and \(Y\) are points on \(QR\) such that \(QY = RX\). Show that \(PX = PY\).
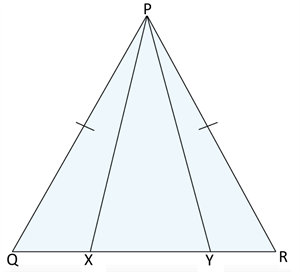
Proof :
In \(∆ PQX\) and \(∆ PRY\),
\(PQ = PR\) ----(1) (Given)
\(∠ Q = ∠ R\) ----(2) ()
That is, \(QX =\) ---- (3)
So, \(∆ PQX ≅ ∆ PRY\) (Using (1), (2), (3) and rule).
This gives \(PX = PY\) (By )
Hence, proved.