\(BA \perp AC\), \(DE \perp DF\) such that \(BA = DE\) and \(BF = EC\). Show that \(\triangle ABC \cong \triangle DEF\).
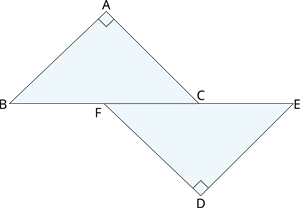
Proof:
Consider \(\triangle ABC\) and \(\triangle DEF\).
\(BA = DE\) [Given]
\(BF = EC\) [Given]
\(\angle A = \angle D = 90^{\circ}\)
Here, \(BC = BF + \) ---- (\(1\))
Also, \(EF = EC + FC\)
\(EF = BF + FC\) [Given that \(BF = EC\)]
\(EF = BC\) [Using equation (\(1\))]
Thus, by rule, \(\triangle ABC \cong \triangle DEF\)
Hence, we proved.