In a garden containing several trees, three particular trees \(P\), \(Q\), \(R\) are located in the following way, \(BP = 2 \ m\), \(CQ = 3 \ m\), \(RA = 10 \ m\), \(PC = 6 \ m\), \(QA = 5 \ m\), \(RB = 2 \ m\), where \(A\), \(B\), \(C\) are points such that \(P\) lies on \(BC\), \(Q\) lies on \(AC\), and \(R\) lies on \(AB\). Check whether the trees \(P\), \(Q\), \(R\) lie on a same straight line.
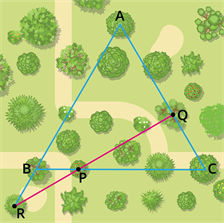
Solution:
By Menelaus theorem:
The trees \(P\), \(Q\) and \(R\) will be collinear if ----------(1)
Substitute the given values in equation (1).
\(=1\)
\(\frac{60}{60} = \)
Hence, the trees \(P\), \(Q\) and \(R\) lies on a same straight line.
Answer variants:
\(\frac{BP}{PC} \times \frac{CQ}{QA} \times \frac{AC}{BC} =1\)
\(\frac{BP}{PC} \times \frac{CQ}{QA} \times \frac{RA}{RB} = 1\)
\(\frac{PC}{BP} \times \frac{CQ}{QA} \times \frac{RA}{BR} = 1\)