Draw a circle of diameter \(6 \ cm\) from a point \(P\), which is \(8 \ cm\) away from its centre. Draw the two tangents \(PA\) and \(PB\) to the circle and measure their lengths.
Construction:
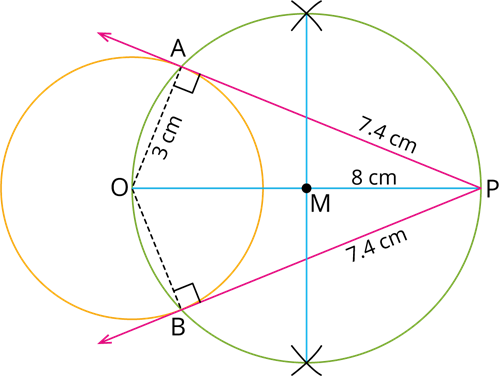
Step 1: With \(O\) as the centre, .
Step 2: Draw .
Step 3: Draw , which cuts \(OP\) at \(M\).
Step 4: With \(M\) as centre and \(MO\) as radius, draw .
Step 5: Join \(AP\) and \(BP\). \(AP\) and \(BP\) are the required tangents. Thus, length of the tangents are \(PA = PB =\) \(\ cm\).
Answer variants:
a circle which cuts previous circle at \(A\) and \(B\)
a circle of radius \(3 \ cm\)
a perpendicular bisector of \(OP\)
\(7.4\)
a line \(OP\) of length \(8 \ cm\)
\(11.2\)