Two circles intersect at two points \(B\) and \(C\). Through \(B\), two-line segments \(ABD\) and \(MBN\) are drawn to intersect the circles at \(A, D\), and \(M, N\) respectively (see below figure). Show that \(∠ACM=∠NCD\).
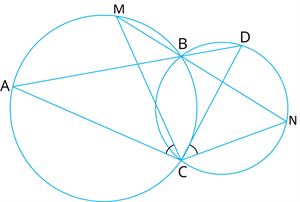
Proof:
Join chords \(AM\) and \(DN\).
For chord \(AM\), \(∠MBA =\) (Angles in the same segment) ... (1)
For chord \(DN\), \(∠DBN =\) (Angles in the same segment) ... (2)
\(ABD\) and \(MBN\) are line segments intersecting at \(B\).
Therefore, \(∠MBA =\) (Vertically opposite angles) ... (3)
From equations (1), (2), and (3),
We obtain \(∠ACM = \)
Hence, proved.