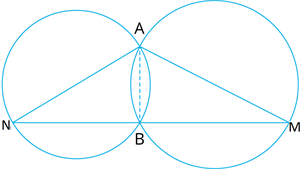
Two circles intersect at two points \(A\) and \(B\). \(AN\) and \(AM\) are diameters to the two circles (see figure). Prove that \(B\) lies on the line segment \(NM\).
Proof:
Now, Join \(AB\).
\(∠ ABN =\) \(^°\) (Angle in a semicircle)
\(∠ ABM =\) \(^°\) (Angle in a semicircle)
So, \(∠ ABN + ∠ ABM =\) \(^°\)
Therefore, \(NBM\) is a line.
That is \(B\) lies on the line segment \(NM\).
Hence, proved.