Graphical representation:
A distance-time graph shows the change in the distance covered by an object with respect to time. It is a pictorial representation of the motion of objects. We choose the convenient scales to plot the axes of the graph.

Object moving with uniform speed
The distance-time graphs are plotted for different scenarios like objects moving with speed at a uniform rate, non-uniform rate, objects at rest, etc.
The speed (v) of the object is given as,
\(v\ =\ \frac{s^2\ −\ s^1}{t^2\ −\ t^1}\)

Object moving with non - uniform speed
This graph shows the non- linear variation of the distance travelled by a vehicle with time (t). The shape of a graph plotted for an object travelling at a non-uniform speed is different from that of the object with uniform speed.
Feroz and his sister Sania go to school on their bicycles. Both of them start at the same time from their home but take different times to reach the school although they follow the same route.

Distance-time graph for their motions
Velocity-time graph:
A velocity-time graph shows the change in the velocity of an object in a straight line with respect to time.

Velocity-time graph
The displacement of an object moving with uniform velocity is the product of velocity and time. The magnitude of displacement is equal to the area enclosed by the velocity-time graph and the time axis in the graph.
The distance covered by the car can also be determined from the velocity-time graph.
The shaded area under the velocity-time graph denotes the magnitude of displacement (distance) travelled by car in a given time interval.

Velocity-time graph for the motion of a car
Equation of motion:
Isaac Newton observed that the motion of an object gives a set of three equations of motion which relates the displacement, velocity, acceleration and time of an object under motion, and these equations are called the equation of motion.
The variables include displacement, velocity, acceleration and time of an object under motion. An object is in motion with initial velocity (u) attains a final velocity (v) in time (t) due to uniform acceleration (a) while covering certain distance (s). The three equations of motion can be written as,
1. \(v\ =\ u\ +\ at\)
2. \(s\ =\ ut\ +\ \frac{1}{2}at^2\)
3. \(v^2\ =\ u^2\ +\ 2as\)
Moving along a closed path:
The athlete runs at constant magnitude along the circular path, the only difference in the velocity occurs due to the change in the direction of motion. As a result, the athlete's motion along a circular path is an example of accelerated motion.
Circumference of a circle of radius, \(r\ =\ 2πr\)
If the athlete completes one round on the circular path of radius r in t seconds, then the speed v is given as,
\(v\ =\ \frac{2\Pi\r}{t}\)
Uniform circular motion:
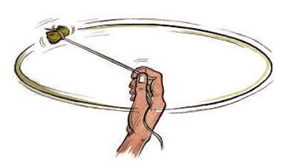
If an object moves with constant speed in a circular path, then the motion is called uniform circular motion.