To describe the position of a point with respect to one line like in the case of a number line is easier. But there are some situations in which we might need to describe the position of a point with respect to more than one line. Thus position of any object lying in a plane can be represented with the help of two perpendicular lines. This given rise to a very important branch of Mathematics known as Coordinate Geometry.
Cartesian system:
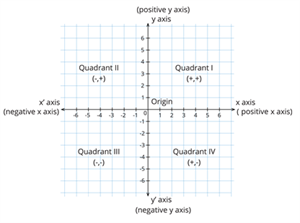
It is a co-ordinate number system used to describe the position of a point in two dimensions by means of two perpendicular lines (x axis and y axis).
The line X′OX is the horizontal line called the x - axis.
The line Y′OY is the vertical line called the y - axis.
Co-ordinate axes:
The plural form of the axis is called the axes. A number line represented horizontally is the x - axis, and a number line represented vertically is the y - axis. Joining both the lines together at origin is called the xy plane or cartesian plane or co-ordinate axes.
In x - axis, the point is positive along the direction OX and negative along the direction OX′.
In y - axis, the point is positive along the direction OY and negative along the direction OY′
Quadrants:
The \(x-axis\) and \(y-axis\) divide the cartesian plane into four regions from the origin. These are called quadrants. They are usually numbered in anticlockwise direction starting from the region bounded by positive \(x\) and \(y\) axis (that is \(OX\)).
Quadrant I:
- Any point located in quadrant \(I\) will have a positive number in the \(x\) - axis and \(y\) - axis.
- That is, \(x > 0\), \(y > 0\).
- The region is \(XOY\).
Example:\((2,3)\), \((6,10)\), \((9,12)\)
Quadrant II:
- Any point located in quadrant \(II\) will have a negative number in the \(x\) - axis and a positive number in \(y\) - axis.
- That is, \(x < 0\), \(y > 0\).
- The region is \(X'OY\).
Example:\((-3,6)\), \((-2,5)\), \((-15,12)\)
Quadrant III:
- Any point located in quadrant \(III\) will have a negative number in the \(x\) - axis and \(y\) - axis.
- That is, \(x < 0\), \(y < 0\).
- The region is \(X'OY'\).
Example:\((-5,-6)\), \((-2,-1)\), \((-8,-10)\)
Quadrant IV:
- Any point located in quadrant \(IV\) will have a positive number in the \(x\) - axis and a negative number in \(y\) - axis.
- That is, \(x > 0\), \(y < 0\).
- The region is \(XOY'\).
Example:\((1,-3)\), \((3, -4)\), \((7,-1)\)