Let us draw a point in the graph. The point is denoted by \((a,b)\), where \(a\) is the distance along the \(X\) - axis and \(b\) is the distance along the \(Y\) - axis. This pair \((a,b)\) is called as the ordered pair. The ordered pair helps us identify the point correctly.
The \(x\) - coordinate in the ordered pair is called abscissa and the \(y\) - coordinate in the ordered pair is called ordinate.
Here, the ordered pair is \((a,b)\), where \(a\) is the \(x\) - coordinate or the abscissa, and \(b\) is the \(y\) - coordinate or the ordinate.
Example:
Let us draw a point in the graph and name it as \(A\). Here, the ordered pair is \((2,5)\).
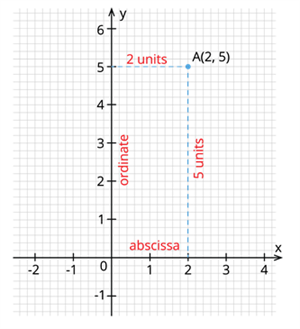
The \(x\) - coordinate or the abscissa of the ordered pair is \(2\) units, and the \(y\) - coordinate or the ordinate is \(5\) units.
Important!
The ordered pairs \((a,b)\) and \((b,a)\) are not same.
Lines parallel to coordinate axes:
Line parallel to the \(x\) - axis:
Consider drawing a line parallel to \(x\)-axis. If the distance from the \(x-axis\) and the line is the same, then the line can be represented as \(y=c\) (where \(c\) is a constant).
Line parallel to the \(x\) - axis:
Consider drawing a line parallel to the \(y\)-axis and the distance between the \(y\)-axis and the line is the same, then the line can be represented as \(x=c\) (where \(c\) is a constant).
Distance between any two points in a cartesian plane:
Consider any two points \(P(x_1,y_1)\) and \(Q(x_2,y_2)\), the distance between any two points can be determined using the formula \(d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}\).