Given two parallel tangents \(XY\) and \(X′Y′\) to a circle with centre \(O\), and a third tangent \(AB\) touching the circle at \(C\) and intersecting the parallels at \(A\) and \(B\). Justify that \(∠AOB\) \(=90^\circ\).
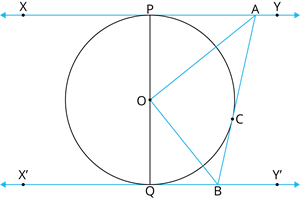
Proof:
As we can observe here, \(AP\) and \(AC\) are tangent at same external point \(A\).
\(QB\) and \(BC\) are tangent at same external point \(B\).
Taking, \(∆OAP\) and \(∆OAC\) in consideration \(OP = OC\) [\(OP\) and \(OC\) radius of the circle]
\(OA\) is the common side.
We know that, The tangent at any point of a circle is perpendicular to the radius through the point of contact.
\(∠OPA = ∠OCA =\) \(^°\)
Therefore by \(SAS\) congruency, \(∆OAP ≅ ∆OAC\)
So, \(∠POA = ∠COA\)
we can conclude that, \(∠COP =\) ----- (1)
Similarly, \(∠COQ =\) ------(2)
Adding (1) and (2), \(RHS = LHS\) we get,
\(2 (∠COA + ∠COB) =\) \(^°\)
\(2 (∠\)\() =\) \(^°\)
\(∠AOB = 90^°\).
Hence, proved.