If a circle is inscribed in a parallelogram. Estimate that the parallelogram is a rhombus.
Proof:
\(ABCD\) is a parallelogram touching the circle at points \(P\), \(Q\), \(R\) and \(S\).
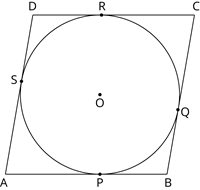
In parallelogram \(ABCD\),
Opposite sides are equal.
\(AB =\) and \(AD =\) - - - (1)
Lengths of tangents drawn from an external point to a circle are equal.
\(AP =\) - - - (2)
\(BP =\) - - - (3)
\(CQ =\) - - - (4)
\(DR =\) - - - (5)
Add equations (2), (3), (4) and (5), we get:
\(AB + CD =\)
Using equation (1),
\(AB =\)
Also \(AB = CD\) and \(AD = BC\)
So, \(AB = BC = CD = AD\).
\(ABCD\) is a parallelogram with .
Hence, \(ABCD\) is a rhombus proved.