If two circles have equal radii and
\(IJ\) and \(KL\)
are their common tangents, show that the lengths of \(IJ\)
and
\(KL\) are equal.
Proof: \(IJ\) and \(KL\) are common tangents to two circles of equal radii.
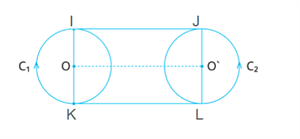
Join \(O\)\(I\), \(O\)\(K\), \(O'\)\(J\) and \(O'\)\(L\).
Tangent at any point on a circle is perpendicular to the radius through the point of contact.
\(O\)\(I\) \(\perp \)\(IJ\) and \(O\)\(K\) \(\perp \)\(KL\)
\(\angle O\)\(IJ\) \(= 90^\circ\) and \(\angle O\)\(KL\) \(= 90^\circ\)
Thus, \(IK\) is a straight line.
Also, \(\angle O'\)\(JI\) \(= \angle O'\)\(LK\) \(= \)\(^\circ\)
Thus, \(JL\) is a straight line.
Therefore, \(IJKL\) is a .
We have, \(\angle\)\(I\) \(= \angle \)\(J\) \(= \angle \) \(K\)\(= \angle\) \(L\) \(= 90^\circ\).
So, \(IJKL\) is a .
Hence, \(IJ\) \(=\) \(KL\).