Prove that points
\(O\), \(F\)
, and
\(O'\)
are collinear, if
\(BC\) and \(DE\)
are common tangents to two circles with centres
\(O\) and
\(O'\), intersects at
\(F\).
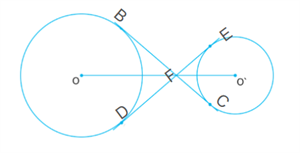
Proof:
\(BC\) and \(DE\) are two tangents with centres \(O\) and \(o'\) intersect at \(F\).
Join \(B\)\(O\), \(O\)\(D\), \(O'\)\(E\) and \(O'\)\(C\).
In \(\Delta O\)\(B\)\(F\) and \(\Delta O\)\(D\)\(F\),
\(O\)\(B\) \(= \) (radii of the same circle)
\(OF\) \(=\) \(OF\) (common side)
\(\angle O\)\(B\)\(F\) \(= \angle\)
Thus, by \(RHS\) congruence criterion, \(\Delta\) \(OBF\)\(\cong \Delta \)\(ODF\)
We know that, corresponding parts of congruent triangles are congruent.
\(\angle\)\(BFO\) \(= \angle \)\(DFO\)
Similarly, \(\angle\)\(CFO'\) \(= \angle \)\(EFO'\)
\(\angle \) \(BFD\)\(= \angle \)
\(\frac{1}{2} \angle\)\(BFD\) \(= \frac{1}{2} \angle \)\(EFC\)
\(\angle \)\(BFO\)\(= \angle\) \(DFO\)\( = \angle \)\(CFO'\)\(= \angle \)\(EFO'\)
Since these angles are equal and are bisected by and \(O'F\),
\(O\), \(F\), \(O'\) are collinear.
Answer variants:
\(OD\)
\(ODF\)
\(EFC\)
\(OF\)