A man is 24.8 \(m\) away from a tower. His eye level above the ground is 1.2 \(m\). The angle of elevation of the top of the tower from his eye is 45\(^{\circ}\). Then find height of the tower, express it in meters
Answer:
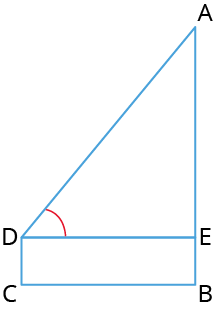
Let \(CD\) denote the eye level of the man from the ground. \(AB\) denotes the height of the tower. Let \(CB\) denote the distance of the man from the tower.
Let the height of the tower be \(AB = h\).
\(AE\) =
In right-angled triangle \(ADE\), \(tan \ \theta = \)
\(tan 45\circ \) =
after simplifying we get
\(h\) =
Answer variants:
\(\frac{DE}{AE}\)
26
28
\(\frac{AE}{DE}\)