A window is at a height
\(
h\) \(\text{metres}\) above the ground. If the angles of elevation and depression of the top and bottom of an opposite house are
\(α\) and
\(
β\), respectively. Prove that the height of the other house is
\(h(1+tan\ α\ cot\ β)\) \(\text{metres}\).
Proof:
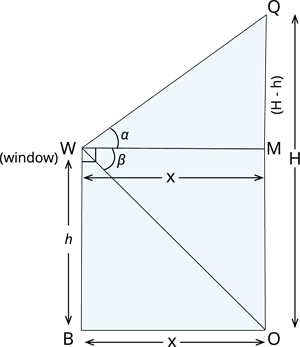
Let \(W\) denote the window, and \(QO\) denote the height of the other house.
Let \(BW = h\), \(BO = WM = x\) and \(QO = H\).
In \(\triangle QWM\), we have:
\(x =\) ---- (\(1\))
In \(\triangle OWM\), we have:
\(x =\) ---- (\(2\))
From equations (\(1\)) and (\(2\)), we have:
\(\frac{H-h}{tan\ \alpha}\) \(=\)
\(H =\)
\(H = h(1 + tan \ \alpha \ cot \ \beta)\)
Hence, we proved.
Answer variants:
\(\frac{h(tan \ \alpha - tan \ \beta)}{tan \ \beta}\)
\(\frac{h}{tan \ \beta}\)
\(\frac{H - h}{tan \ \alpha}\)
\(\frac{h(tan \ \alpha + tan \ \beta)}{tan \ \beta}\)