The lower window of a house is at a height of \(2 \ m\) above the ground and its upper window is \(4 \ m\) vertically above the lower window. At certain instant the angles of elevation of a balloon from these windows are observed to be \(60^{\circ}\) and \(30^{\circ}\), respectively. Find the height of the balloon above the ground.
Answer:
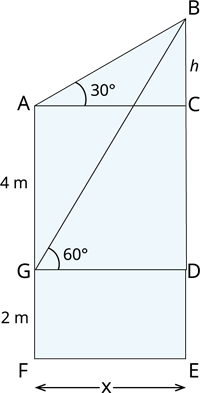
Let \(G\) denote the lower window, and \(A\) denote the upper window of the house. The angle of elevation of the balloon from the lower window and upper window of the house are \(60^{\circ}\) and \(30^{\circ}\), respectively.
In \(\triangle BAC\), \(tan \ \theta =\)
From this, \(x=\)
\(tan \ 60^{\circ} =\)
From this, \(x=\)
The height of the balloon \(=\) \(m\)