In a quadrilateral, a point \(
X\) is chosen and lines through it are drawn parallel to
\(CB\) and
\(
CD\). These lines meet
\(AB\) at \(Y
\) and
\(AD\) at
\(Z\). Show that the ratios \(\frac{AY}{AB}=\frac{AZ}{AD}\) are equal.
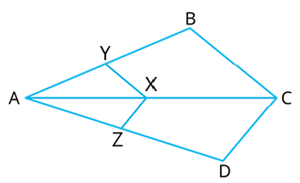
Proof:
In \(\Delta ACB\),
\(XY || CB\)
If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.
\(\frac{AX}{XC} =\) - - - - (1)
In \(\Delta ACD\),
\(XZ || CD\)
If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.
\(\frac{AX}{XC} =\) - - - - (2)
From (1) and (2),
\(\frac{AY}{YB} = \)
\(\frac{YB}{AY} = \)
Simplifying we get,
\(\frac{AY}{AB} = \frac{AZ}{AD}\)
Hence proved.
Answer variants:
\(\frac{BX}{XA}\)
\(\frac{AY}{YB}\)
\(\frac{AZ}{ZD}\)
\(\frac{ZD}{AZ}\)