Let \(ABCD\) be a quadrilateral such that the diagonal \( BD \) is the internal bisector of both \( \angle B \) and \( \angle D \). Determine that:
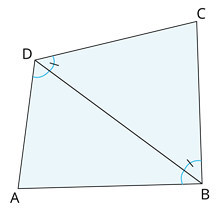

(i) \(\Delta ABD \sim \Delta CBD\)
(ii) \(AB=BC\)
Proof:
\(\angle ADB =\) ()
\(\angle ABD =\) ()
Thus, \(\Delta ABD \sim \Delta CBD\) [by ].
Then corresponding sides are proportional to each other,
\(\frac{AB}{BC}=\frac{BD}{BD}\)
\(\Rightarrow \frac{AB}{BC}=1\)
\(\Rightarrow AB = BC\).