In the adjoining figure, \(\Delta CAB\) is a right triangle, right angled at \(A\) and \(AD \perp BC\). Show that \(\Delta ADB \sim \Delta CDA\). Further, if \(BC = 37 \ cm\) and \(CD = 1 \ cm\), determine the length of \(AD\).
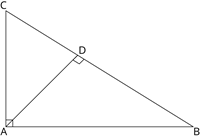

Let \(\angle CAD = x\) and \(\angle DAB = 90^\circ - x\)
\(\angle DBA = 180^\circ - (90^\circ + 90^\circ - x) = x\)
So, \(\angle CAD = \) - - - (i)
In \(\Delta ADB\) and \(\Delta CDA\),
\(\angle D = \) ()
\(\angle DBA = \angle CAD\) (using (i))
Thus, \(\Delta ADB \sim \Delta CDA\) (by ).
In similar triangles, the corresponding sides are in proportion.
\(\frac{AD}{CD} = \)
By simplifying the above ration we get, .