In given figure, \(l || m\) and line segments \(AB\),\(DE\) and \(EF\) concurrent at point \(P\). Prove that \(\frac{AE}{BF} = \frac{AC}{BD} = \frac{CE}{FD}\).
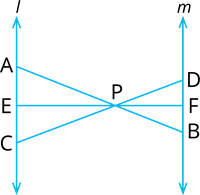
In \(\Delta APC\) and \(\Delta BPD\),
\(\angle APC = \angle BPD\) (vertically opposite angles)
\(\angle PAC = \angle PBD\) (alternate angles)
Therefore, \(\Delta APC \sim \Delta BPD\) (by \(AA\) similarity criterion)
\(\frac{AP}{PB} = \frac{AC}{BD} =\) - - - - (i)
In \(\Delta APE\) and \(\Delta BPF\),
\(\angle APE = \angle BPF\) (vertically opposite angles)
\(\angle PAE = \angle PBF\) (alternate angles)
Therefore, \(\Delta APE \sim \Delta BPF\) (by \(AA\) similarity criterion)
\(\frac{AP}{PB} = \frac{AE}{BF} = \) - - - - (ii)
In \(\Delta PEC\) and \(\Delta PFD\),
\(\angle EPC = \angle FPD\) (vertically opposite angles)
\(\angle PCE = \angle PDF\) (alternate angles)
Therefore, \(\Delta PEC \sim \Delta PFD\) (by \(AA\) similarity criterion)
\(\frac{PE}{PF} = \frac{PC}{PD} =\) - - - - (iii)
From equation we gert the result.