In the given figure, \(ABC\) and \(AMP\) are two right triangles, right angled at \(B\) and \(M\) respectively. Prove that:
(i) \(\Delta ABC \sim \Delta AMP\)
(ii) \(\frac{CA}{PA} = \frac{BC}{MP}\)
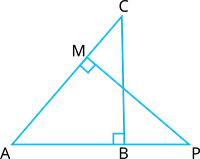
(i) Given \(ABC\) and \(AMP\) are two right triangles, \(\angle = 90^\circ\), \(\angle AMP = 90^\circ\)
In \(\Delta ABC\) and \(\Delta AMP\),
\(\angle CAB = \angle\) (Common angle)
\(\angle ABC = \angle\) (Both \(90^\circ\))
Thus, \(\Delta ABC \sim \Delta AMP\) ( similarity)
(ii) In the first part we proved, \(\Delta ABC\) and \(\Delta AMP\)
If two triangles are similar, then the ratio of their corresponding sides is proportional.
\(\frac{CA}{PA} = \frac{BC}{MP} =\)
Hence, we get the result.