In the given figure, \(A\), \(B\) and \(C\) are points on \(OP\), \(OQ\) and \(OR\) respectively such that \(AB||PQ\) and \(AC||PR\). Show that \(BC||QR\).
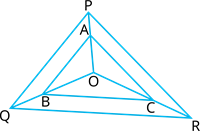
Proof:
In \(\Delta OPQ\),
\(AB || PQ\)
If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.
\(\frac{OA}{AP} =\) - - - - (1)
In \(\Delta OPR\),
\(AC || PR\)
If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.
\(\frac{OC}{CR} = \) - - - - (2)
From (1) and (2),
\(\frac{OC}{CR} = \)
In \(\Delta OQR\),
\(\frac{OC}{CR} = \)
If a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side.
Thus, \(BC||QR\).
Hence proved.