The sides of the triangle can neither be too long or too short with respect to the other two sides.
Earlier, we have discussed the triangle inequality for the sum of two sides. The sum inequality ensures that the two sides can physically meet to form a vertex.
To ensures that neither of the two sides of the triangle is long enough to overpower the third side from forming a triangle, we will learn the triangle inequality for the difference of two sides.
Triangle inequality for the difference of two sides:
In any triangle, the difference in the length of any two sides of a triangle is always lesser than the third side.
Mathematical notation for triangle inequality:
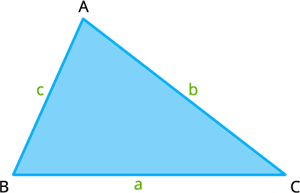
For any triangle \(\Delta ABC\) with sides \(a\), \(b\) and \(c\) opposite to vertices \(A\), \(B\) and \(C\) respectively, the triangle inequality states that:
\(a - b < c\)
\(b - c < a\) and
\(c - a < b\)
Example:
Consider the triangle\(ABC\) whose sides measures are \(AB = c = 3 cm, BC = a = 4 cm\) and \(AC = b =5 cm\).
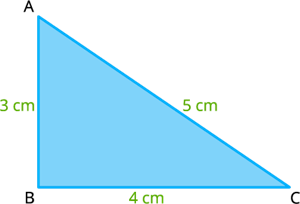
Let's check the triangle inequality for the triangle \(ABC\),
\(a - b = 4 - 5 = -1 < 3 = c\)
\(b - c = 5 - 3 = 2 < 4 = a\) and
\(c - a = 3 - 4 = -1 < 5 = b\)
Important!
Suppose \(a, b\) and \(c\) are the sides of a triangle with \(a\) and \(b\) are known sides and \(c\) is unknown. We use the triangle inequality to find the third side \(c\). As the sum of two sides\((a+b)\) of a triangle is always greater than the third side\((c)\), and difference of two sides\((a-b)\) of a triangle is always lesser than the third side\((c)\), the length of the third side\((c)\) must lie between difference\((a-b)\) and sum\((a+b)\).
The three line segments form a triangle if and only if each side lies between the difference and the sum of the other two sides.