The triangle inequality is a fundamental property of triangles in geometry. It provides a necessary and sufficient condition for three line segments to form a triangle. This principle is widely used in geometric constructions.
Triangle Inequality for sum of two sides:
The sum of the length of any two sides of a triangle is always greater than the length of the third side.
Mathematical notation for triangle inequality:
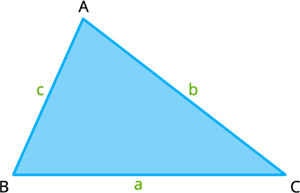
For any triangle \(\Delta ABC\) with sides \(a\), \(b\) and \(c\) opposite to vertices \(A\), \(B\) and \(C\) respectively, the triangle inequality states that:
\(a + b > c\)
\(b + c > a\) and
\(c + a > b\).
These inequalities must hold simultaneously for a triangle to exist.
Converse of the triangle inequality:
If any three positive numbers \(a\), \(b\) and \(c\) satisfy the triangle inequalities:
\(a+b>c\),
\(a+b>c\),
\(b+c>a\), and
\(c+a>b\),
then it is always possible to construct a triangle with sides \(a\), \(b\) and \(c\).
then it is always possible to construct a triangle with sides \(a\), \(b\) and \(c\).
This result is central to geometric constructions with a compass and ruler.
Example:
Consider the triangle \(ABC\) with sides measures \(AB = c = 3 cm, BC = a = 4 cm\) and \(AC = b = 5 cm\).
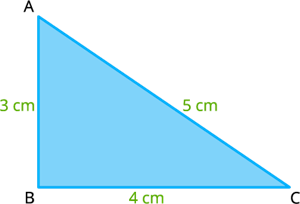
Let's check the triangle inequality for the triangle \(ABC\),
\(a + b = 4 + 5 = 9 > 3 = c\)
\(b + c = 5 + 3 = 8 > 4 = a\) and
\(c + a = 3 + 4 = 7 > 5 = b\).