Expression:
We would have come across many expressions in mathematics such as \(3 + 2\), \(6 - 4\) and so on.
In algebra, such expressions are written using symbols.
An expression is a combination of variables and constants.
An algebraic expression can be both a combination of variables and constants or wholly variables.
Example:
\(2x\) \(+\) \(3\), \(3x\) \(+\) \(4y\) and so on.
Let us look at a few more expression:
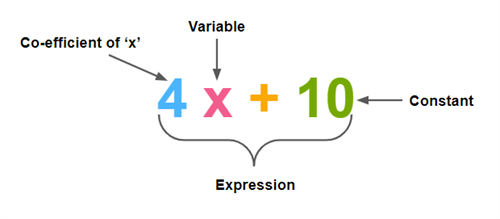
Consider \(4x + 10\):
\(4\) is the co-efficient of '\(x\)'.
\(x\) is the variable.
\(10\) is the constant.
\(4x + 10\) is altogether an expression.
Letter-numbers and algebraic expressions:
Letters that are used to represent numbers are called letter-numbers.
Mathematical expressions that contain letter-numbers are called algebraic expressions.
An algebraic expression is formed by combining letter-numbers and numbers using mathematical operations such as addition, subtraction, multiplication, or division.
For example, if \(a\) represents Aftab’s age, then Shabnam’s age, which is \(3\) years more than Aftab’s age, can be written as the algebraic expression \(a+3\).
Formation of an expression:
An expression can also be written in words.
Let us look at a few expressions and their definitions.
|
Expression
|
Definition
|
|
\(x + 3\)
|
\(3\) added to \(x\) |
|
\(2x\)
|
\(2\) times \(x\) |
|
\(4x + 2y\)
|
First \(x\) is multiplied by \(4\) and is added to \(y\) multiplied by \(2\) |
|
\(-5p\)
|
\(p\) multiplied by \(-5\) |
Let us look at an example based on the formation of expression.
How do you define \(6x + 4y\)?
It is defined as '\(x\) multiplied by \(6\) and added to \(y\) multiplied by \(4\)'.
Simplifications of expressions:
When an algebraic expression contains many terms, it may look lengthy or complicated.
By simplifying it, we collect similar terms together and reduce the expression to its simplest form.
For example:
\(3x+5x\) can be simplified to \(8x\).
\(4a+2b−a\) can be simplified to \(3a+2b\).