
In a circle, chords \(AB\) and \(CD\) are equal and, when produced, intersect at \(R\). Verify that \(RB=RD\)
Explanation:
Now, Join \(OR\), draw \(OL⊥ AB\) and \(OM⊥ CD\).
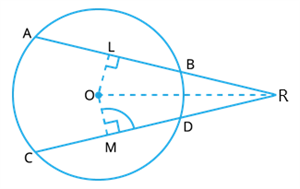
Here, \(AB = CD\).
Therefore, \(OL = \) []
In \(△OLR\) and \(△OMR\),
\(OL =\)
\(∠OLR=∠\) [] and
\(OR= \)\(OR\) []
Therefore, \(△OLR≅△OMR\) [RHS congruence rule]
Now, \(LR = \)\(MR\) [by ] .....(1)
Now, \(AB = CD\).
\(\frac{1}{2}AB=\frac{1}{2}CD\)
\(BL=\) .....(2)
[]
On subtracting (2) from (1) , we get
\(LR − BL = MR − DM\)
Therefore, \(RB = RD\)
Hence, proved.