
Show that if two circles have the same radius, then their equal chords form equal angles at the centres.
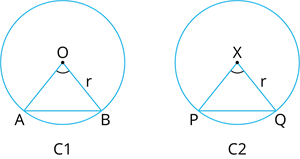
Given: Two Congruent Circles \(C_1\) and \(C_2\)
\(AB\) is the chord of \(C_1\) and
\(PQ\) is the chord of \(C_2\)
Also, \(AB =PQ \)
To Prove: Angle subtended by the Chords AB and PQ are equal
That is, \(∠AOB = ∠PXQ\)
Proof:
In \(△AOB\) and \(△PXQ\)
\(AO =\) ()
\(BO =\) ()
\( AB=\) (Given)
\(△AOB ⩭ △PXQ\) ()
Therefore, \(∠AOB = ∠PXQ\) ()
Answer variants:
AQ
\(PX\)
\(QX\)
\(PQ\)