
Prove that in congruent circles, chords which make equal angles at the centres are equal in length.
Proof:
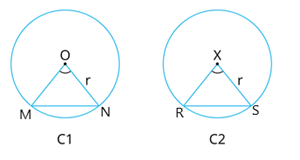
Given: Two Congruent Circles \(C_1\) and \(C_2\)
\(MN\) is the chord of \(C_1\) and
\(RS\) is the chord of \(C_2\)
Also, \( ∠MON = ∠RXS \)
Proof:
In \(△MON\) and \(△RXS\),
\(MO =\) ()
\(∠MON = ∠\) (Given)
\(NO = \) ()
\(△MON ⩭ △RXS\) ()
Therefore, \(MN= \) ()