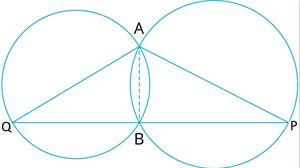
Two circles intersect at two points \(A\) and \(B\). \(AQ\) and \(AP\) are diameters to the two circles (see given figure). Check that \(B\) lies on the line segment \(QP\).
Proof:
Now, Join \(AB\).
\(∠ ABQ =\) \(^°\) (Angle in a semicircle)
\(∠ ABP =\) \(^°\) (Angle in a semicircle)
So, \(∠ ABQ + ∠ ABP =\) \(^°\)
Therefore, \(QBP\) is a line.
That is \(B\) lies on the line segment \(QP\).
Hence, proved.