In the following figure, \(AB\) is a diameter of the circle, \(CD\) is a chord equal to the radius of the circle. \(AC\) and \(BD\) when extended intersect at a point \(P\). Check that \(∠ AB = 60^°\).
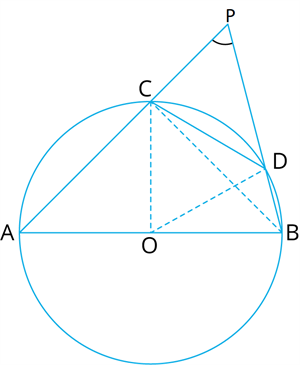
Proof:
Join \(OC\), \(OD\) and \(BC\).
Triangle \(ODC\) is equilateral.
Therefore, \(∠ COD =\) \(^°\)
We know that, The angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle.
Therefore, \(∠ CBD = \frac{1}{2} ∠\)
This gives \(∠ CBD =\) \(^°\)
Again, \(∠ ACB =\) \(^°\)
So, \(∠ BCP = 180^° – ∠ ACB =\) \(^°\)
Which gives \(∠ CPB = 90^° – 30^° = 60^°\)
That is, \(∠ APB = 60^°\)
Hence, proved.